|
Nous amènerons
les positions principales de la décomposition nodale et le calcul par
parties.
La composition
des sous-schémas est définie "à la main". L'information sur les
sous-schémas consiste en l'information sur les branches et les matrices
de changement de bases.
Le calcul du
grand schéma commence par le calcul des sous-schémas. Les sous-schémas
séparés calculent indépendamment une de l'autre:

On introduit
les résistances des liens joignant les sous-schémas dans les noeuds:

On résout
alors le calcul du schéma total dans l'espace des mailles, et pour
terminer on prend en considération l'influence mutuelle des sousschémas:
Les schémas équivalents les suivants:
Au calcul des sous-schémas indépendants on accomplit le
calcul des schémas radiaux équivalents pour les sous-schémas et tensions
sur les noeuds de frontière:

Les résistances des liens forment le réseau dit des
intersections :
Après une dernière étape de liaison des branches
appartenant du réseau des intersections, on forme le schéma total, sa
dimension étant moins grande que la dimension du schéma complet:

Nous examinerons plus en détail les étapes du calcul
Nous allons examiner l’exemple présenté fig. 1.
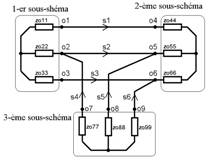
Figure 1: exemple de la liaison
de trois sous-schémas
Le calcul du grand schéma commence par le
calcul des sous-schémas. Puisque les phénomènes électromagnétiques sont
décrits dans l'espace des mailles, le calcul est accompli dans cet
espace. L'espace des branches généralisées est donné par le vecteur du
courant dans les branches, l'espace du schéma élaboré est donné par le
vecteur des courants des mailles. Ce vecteur s’obtient par
transformation via la matrice de changement de base (connectivité) de
l’espace des branches vers l’espace des mailles. Les coordonnées nodales
classiques sont présentées comme des mailles ouvertes. Les coordonnées
nodales sont nécessaires à l'algorithme de formation automatique des
équations du schéma à partir des sous-schémas :
|
|
|
|
|
|
o |
m |
|
|
|
|
|
|
Eo |
+ |
eo |
= |
o |
zoo |
zom |
∙( |
0 |
+ |
Io |
) |
|
0 |
em |
m |
zmo |
zmm |
im |
Im |
De cette équation, on obtient
l'expression des tensions nodales Eo:
Eo =
z~oo
Io
−
e~o
,
où e~o = eo
−
zom
(zmm)-1
em
,
(1)
z~oo
=
zoo
–
zom
(zmm)-1
zmo
(2)
Après application des équations (1) et
(2) aux sous-schémas, on en déduit les schémas équivalents radiaux de
ces sous-schémas (par exemple, comme sur la fig. 2).

Figure 2: exemple du schéma équivalent radial du
sous-schéma.
Nous reviendrons vers les
fig 1. Les sous-schémas, qui sont amenés sur le
fig. 1 sont présentés comme les sous-schémas radiaux. On peut diviser en
trois groupes les liens qui forment le réseau des intersections. Au
premier groupe se rapportent les branches s1, s2
et s3, au deuxième groupe se rapportent la branche
s4, au troisième groupe se rapportent les branches s5
et s6. On en déduit la matrice d’incidence décrivant le
réseau d’intersections
:
|
|
|
s1 |
s2 |
s3 |
s4 |
s5 |
s6 |
|
|
o1 |
-1 |
|
|
|
|
|
|
|
o2 |
|
-1 |
|
1 |
|
|
|
|
o3 |
|
|
-1 |
|
|
|
|
|
o4 |
1 |
|
|
|
|
|
|
Cōs
= |
o5 |
|
1 |
|
|
1 |
|
|
|
o6 |
|
|
1 |
|
|
1 |
|
|
o7 |
|
|
|
-1 |
|
|
|
|
o8 |
|
|
|
|
-1 |
|
|
|
o9 |
|
|
|
|
|
-1 |
La matrice des
impédances du réseau d’intersections
zss
est calculée par la transformation standard de la matrice des impédances
de noeuds de frontières
zss
=Csō
∙
z~ōō
∙ Cōs
En analysant le contenu
de la matrice
zss,
on voit que cette matrice reflète le schéma présenté fig. 3. Nous
pouvons alors calculer la source de tension pour chaque branche de
réseau élémentaire des intersections. Cette source se forme aussi par
une transformation classique :
es
= − Csō
∙ Eō.
Nous avons établi qu'entre chaque couple
de sous-schémas on peut choisir une branche totale.
Sur la fig.3 ces branches totales sont
s3, s4 et s5. Les autres
branches : s1, s2, s6 - sont
des branches dites complémentaires.
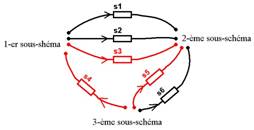
Figure 3 : réseau des interconnexions. On met en relief
les branches totales.
Entre chaque couple de sous-schémas
voisins se forme un réseau d’échange ou « réseau de circulation ». Les
branches totales forment l'arbre couvrant, les autres branches forment
les mailles du réseau de circulation. La matrice décrivant le réseau de
circulation est :
|
|
|
s3 |
s4 |
s5 |
s1 |
s2 |
s6 |
|
|
s1 |
|
|
|
1 |
|
|
|
|
s2 |
|
|
|
|
1 |
|
|
Csa
= |
s3 |
1 |
|
|
-1 |
-1 |
|
|
|
s4 |
|
1 |
|
|
|
|
|
|
s5 |
|
|
1 |
|
|
-1 |
|
|
s6 |
|
|
|
|
|
1 |
Maintenant,
nous utiliserons uniquement les branches totales et nous laisserons
toutes les autres branches. Nous voyons que les branches totales
s3, s4 et s5 forment un certain
schéma indépendant, vers lequel les contours et les « paires de nœuds »
entrent (Fig.4).
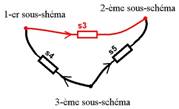
Figure 4: Le réseau total
Le schéma total reflète la structure de la liaison des sous-schémas.
Cette structure est beaucoup plus simple que celle du schéma complet. On
peut trouver dans le réseau total de la fig.3 de nouveau deux branches
d’un arbre couvrant et une branche complémentaire. Par exemple, on
retient les branches de l'arbre s4 et s5,
s3 devenant la branche complémentaire. Le schéma n’étant plus
réductible, on peut définitivement énumérer toutes les branches des
compléments : s1, s2, s6, s3
et les branches de l'arbre couvrant total : s4 et s5.
La matrice orthogonale reflétant les liaisons des branches du réseau
d’intersections au schéma total s’en déduit :
|
|
s4 |
s5 |
s3 |
s1 |
s2 |
s6 |
|
s3 |
|
|
1 |
|
|
|
|
s4 |
-1 |
|
1 |
|
|
|
|
Cap
= s5 |
|
-1 |
-1 |
|
|
|
|
s1 |
|
|
|
1 |
|
|
|
s2 |
|
|
|
|
1 |
|
|
s6 |
|
|
|
|
|
1 |
Pour le
calcul par la méthode des courants de mailles, on peut mettre en relief
dans la matrice Cap
la sous-matrice des contours fermés Capm.
Elle est faite des colonnes des branches des compléments
s1,
s2, s6, s3:
|
|
s3 |
s1 |
s2 |
s6 |
|
s3 |
1 |
|
|
|
|
s4 |
1 |
|
|
|
|
Capm
= s5 |
-1 |
|
|
|
|
s1 |
|
1 |
|
|
|
s2 |
|
|
1 |
|
|
s6 |
|
|
|
1 |
D’où l’on déduit :
Cōpm=
Cōs∙Csa∙Capm
(3)
La matrice des
impédances des mailles du schéma complet s’écrit de fait :
zpmpm
= Сpmō
∙ zōō
∙ Cōpm.
(4)
et le vecteur des forces électromotrices
des mailles:
epm=
-Cpmō
∙ Eō.
(5)
On calcule la
matrice inverse :
ypmpm
= (zpmpm)-1
(6)
Le vecteur des
courants des mailles se trouve suivant la relation :
ipm=
ypmpm
∙ epm.
(7)
Le calcul des
courants ipm
peut être accompli par la méthode du Gauss, en utilisant l'équation:
epm=
zpmpm
∙ ipm.
(7)'
Dans ce cas le
calcul de la matrice inverse ne se pose pas. Les courants dans les liens
sont calculés à partir des courants de mailles précédemment trouvés:
is
= Cspm
∙ ipm.
(8)
Les courants des
branches du lien, qui vont aux sous-schémas, se manifestent comme les
courants supplémentaires dans les noeuds de frontière des sous-schémas.
Ceci est la conséquence de la relation:
ΔIō
= Cōs
∙ is.
(9)
En raison de
l'apparition de courants supplémentaires dans les noeuds, il y a
accroissement des tensions nodales dans les sous-schémas:
ΔEo=
zoō
∙ ΔIō.
(10)
Les courants
supplémentaires s’en déduisent également dans les mailles des
sous-schémas:
Δim
= -(zmm)-1
∙ zmō
∙ ΔIō
(11)
Les tensions aux
noeuds et les courants de mailles des sous-schémas s’expriment alors par
:
Ĕo
= Eo
+ ΔEo.
(12)
ĩm
=i m
+ Δim
(13)
De ces
expressions, on obtient les tensions et courants définitifs des
branches des sous-schémas:
Eb=
Аbo
∙ Ĕo,
(14)
ib
= Cbō
·
ΔIō
+ Cbm
∙( Im+ĩm).
(15)
Cette dernière
relation conclue le calcul du grand schéma par la méthode diakoptique.
Les résultats obtenus peuvent être
appliqués pour l'étude des réseaux avec des structures variables pour la
liaison des sous-schémas. Les branches du lien (par exemple, s1-s6
sur le fig. 1) se présentent comme des clés
idéales qui rompent le réseau en circuit-ouvert dans l'état
non-conducteur et deviennent en court-circuit dans l'état passant. La
structure du réseau totale (par exemple, sur la
fig.4) reste invariable, mais l'algorithme doit prévoir le choix
automatique des nouvelles branches totales dans le réseau
de circulation.
Dans les rapports amenés on
accepte les indices suivants:
b - Les coordonnées
des branches de sous-schémas
m - Les coordonnées
des mailles de sous-schémas,
o - Les coordonnées
des noeuds de sous-schémas,
ō - Les coordonnées
des noeuds de frontière,
s -
Les coordonnées des réseau intersections,
a -
Les coordonnées des réseau
circulation
рm
- Les coordonnées des mailles de réseau total.
L’utilisation de la diakoptique
pour la parallélisation apparaît comme une évidence: on accomplit parallèlement le calcul
des sous-schémas séparés. Les résultats du calcul des impédances des noeuds aux
frontières sont ensuite soumis à un processeur principal qui accomplit alors le
calcul du schéma total. Le résultat du calcul est le vecteur des courants de
mailles du schéma total. Leurs valeurs sont redistribuées par le processeur
principal aux autres processeurs. Ensuite on effectue le calcul parallélisé des
sous-schémas en tenant compte des courants ajoutés au schéma total. Un tel
algorithme demande des dépenses minima en temps de transmission de données entre
les processeurs.
Dans le tableau 1 on présente les étapes principales de l'algorithme. Les
lignes obscurcies (4, 5, 7, 8, 11) correspondent à la partie séquentielle de
l'algorithme. Les lignes (1, 2, 6, 10) correspondent à la partie parallélisée de
l'algorithme. Les lignes 3 et 9 correspondent à l'envoi des données entre les
cœurs. Dans le tableau, dans les lignes 5 et 8, on présente deux variantes de
l'algorithme. La variante de gauche correspond au calcul de la matrice inverse
des résistances linéaires du schéma total. La variante de droite correspond au
calcul du schéma total par la méthode du Gauss.
|
№ |
Nom
de l'étape |
Formule |
|
1 |
L'entrée du schéma et des
sous-schémas |
|
|
2 |
Calcul des résistances des
sous-schémas. Séparation des résistances de frontière des
sous-schémas |
z~oo
=
zoo
–
zom
∙
(zmm)-1
∙ zmo |
|
3 |
Collecte d'information sur les
résistances de frontière |
|
|
4 |
Formation de la topologie du
schéma total |
Сōpm=
Сōs
∙
Сsa
∙
Сapm
|
|
5 |
Formation des matrices des
résistances du schéma total |
zpmpm
=
Сpmō
∙ z~ōō
∙ Cōpm
ypmpm
= (zpmpm)-1 |
zpmpm
=
Сpmō
∙ z~ōō
∙ Cōpm |
|
6 |
Calcul des tensions nodales
des sous-schémas |
Eo
=
z~oo
∙
Io
−
e~o
,
où e~o
= eo
−
zom
∙
(zmm)-1
∙
em |
|
7 |
Calcul des fem de mailles du
schéma total |
epm=
-Cpmō
∙ Eō
|
|
8 |
Calcul des courants du schéma
total |
ipm=
ypmpm
∙ epm
|
epm=
zpmpm
∙ ipm
|
|
9 |
Envoi des
résultats im |
|
|
10 |
Calcul des accroissements des
courants de nœuds.
Calcul de la réponse
définitive. |
is
= Cspm
∙ ipm
ΔIō
= Cōs
∙ is
ΔEo=
z~oō
∙
ΔIō
Δim
= -(zmm)-1
∙
zmō
∙
ΔIō
Ĕo=Eo+ΔEo
ĩm=im+Δim
Eb=
Аbo∙
Ĕo
ib=Cbō
·
ΔIō
+
Cbm
∙ (Im
+
ĩm) |
|
11 |
Enregistrement des résultats du
calcul |
|
Le logiciel est
programmé sur Intel Fortran Compiler XE 12.0. Pour la programmation parallèle on
utilise la technologie coarray Fortran. Cette technologie est très simple
pour la programmation de l'échange des données entre les processeurs.
Le
logiciel était testé pour 32-cœurs et 40-cœurs d'architecture Intel. Au cours du
test on fixait le temps de calcul et les caractéristiques principales des
calculs parallélisés. L'accélération est calculée selon la formule A = (N • Tp +
Ts)/(Tp +Ts), où Ts est le temps de calcul de la partie séquentielle du
programme, Tp - le temps de calcul de la partie parallélisée du programme et N -
le nombre de cœurs (sous-schémas). L'efficacité est calculée selon la formule :
Е=А/N.
Nous amènerons ces caractéristiques principales pour le procès du calcul des
schémas (dans le domaine de fréquence) à l'augmentation de la dimension du
schéma au détriment de l'augmentation du nombre de sous-schémas de 4 jusqu'à 40
(et en conséquence du nombre de cœurs). Les résultats sont amenés sur la figure
disposée ci-dessous:
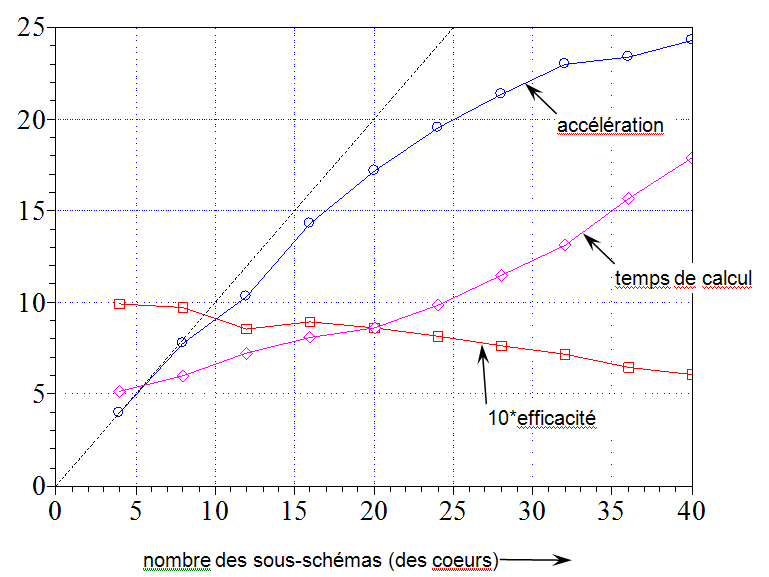
Comme on voit sur la figure, pour le schéma comprenant 40 sous-schémas (le
schéma est amené à la page "Les calculs
parallèles"), l'accélération est égale 24, l'efficacité est 0.6, le
temps de calcul est 18 sec. Les dépenses du temps pour chaque étape du calcul de
ce schéma sont amenées sur le diagramme circulaire ci-dessous (les noms des
étapes correspondent au tableau):

Cet variant correspond au calcul des courants du schéma total par la méthode du
Gauss (l'étape 9). Sur le diagramme les segments avancés correspondent aux
parties successives de la logicielle.
La charge sur les
cœurs séparés est amenée sur la figure ci-dessous:

Sur la figure du numéro des étapes correspondent aux numéros sur le diagramme
circulaire. Le symbole 'р' correspond à la partie parallèle du programme, le
symbole 's' correspond à la partie successive du programme. Les 5-ème et 6-ème
étapes demandent une certaine explication. Dans le tableau et sur les dessins
amenés ils sont marqués comme les étapes, qui sont accomplies successivement. En
effet, pour l'exécution de ces étapes assez d'un cœur. Mais la réalisation d'un
tel moyen demandera ensuite les diffusions des résultats sur les autres coeurs.
Il se trouva que les dépenses du temps pour la diffusion sont proportionnées aux
dépenses du temps pour les calculs. C'est pourquoi en réalité les étapes 5 et 6
sont accomplies simultanément sur tous les cœurs.
Sur les diagrammes on voit que le temps principal de la partie successive du
programme est dépensé sur le calcul du schéma total. Dans les schémas contenant
un plus petit nombre des sous-schémas, la dimension du schéma total même est
moins. Donc, le temps de la partie successive du programme diminue. Cela amène à
l'augmentation de l'efficacité des calculs.
|